Le chiffrement homomorphe permet de travailler sur des données chiffrées sans avoir à les déchiffrer. Comment cette technologie s’applique- t-elle à la sécurité du Cloud ? Quel est son état de l’art ?

Le cloud public est une solution merveilleuse pour stocker les données. Pour un coût de services maitrisé, les entreprises ont la possibilité de disposer de tout l’espace qui leur est nécessaire, sans avoir à investir sur des serveurs et des disques supplémentaires, quand un besoin de plus d’espace de stockage apparait.

Comme la sécurité n’est pas, dans la plupart des cas, le métier des entreprises utilisatrices des services du Cloud, celles-ci peuvent s’assurer, par contrat, que leurs données sont bien en sécurité dans le cloud de leur prestataire. Voilà pour la disponibilité des données et leur protection périmétrique. Quand les entreprises ne maîtrisent pas la sécurité et la sûreté de leurs données numériques, celles-ci font face à de multiples menaces et rares sont les entreprises en mesure de les contrer efficacement. Les prestataires de cloud sont par contre censés bien maîtriser la cybersécurité et censés avoir les compétences dans ce domaine.

Mais qu’en est-il de la confidentialité et de l’intégrité des données confiées dans un cloud extérieur ?

Rappelons que la confidentialité d’une information est l’assurance qu’elle ne pourra être lue que par des personnes autorisées à en prendre connaissance, alors que l’intégrité est l’assurance qu’elle ne peut être écrite ou modifiée que par les personnes également autorisées à le faire.

Une solution serait de n’utiliser l’espace d’un cloud public que pour héberger les données non sensibles. Mais alors on se prive de l’avantage de l’espace quasi infini que propose le cloud pour les héberger. Chiffrer les données sensibles et les confier dans un cloud public est aussi une solution, mais qui gère les clés ? L’idéal est bien sûr, pour les entreprises qui confient leurs données dans un Cloud public, de gérer elles-mêmes les clés de chiffrement. Confier la gestion des clés de chiffrement à son prestataire de cloud trouve ses limites dans la confiance que les entreprises clientes accordent à leur prestataire. Gérer les clés de chiffrement en interne dans l’entreprise est une tâche complexe pour qui la sécurité des données numériques n’est pas le métier. Confier la gestion des clés à un autre prestataire différent de celui qui héberge les données chiffrées semble être une meilleure solution. La confidentialité et l’intégrité des données sensibles sont ainsi assurées.

Si les données sont stockées en clair chez le prestataire, alors le client peut en disposer pour effectuer des traitements mais elles sont accessibles à toute personne mal intentionnée disposant d’un accès privilégié chez le prestataire. Si les données sont stockées chiffrées, il est alors difficile d’en disposer pour effectuer des traitements.

Le problème qui se pose est donc : « comment effectuer des traitements sur les données chiffrées ? ». Il est bien évident que, par exemple pour une addition entre deux nombres qui sont chiffrés, la somme des deux nombres chiffrés ne donne pas, lors du déchiffrement, le résultat attendu. Il est bien sûr possible de rapatrier en internes les données à traiter, les déchiffrer pour effectuer les traitements, chiffrer les résultats et les remettre éventuellement dans le Cloud. Cette solution n’est, de toute évidence, pas vraiment jouable.

Alors le Cloud est-il condamné à ne rester qu’un espace de stockage, sans permettre un espace de calcul ? Les données à manipuler ne pourraient- elles pas rester dans le Cloud, chiffrées, et les traitements s’effectuer sur les données chiffrées en donnant le bon résultat lors du déchiffrement chez l’utilisateur ?

Il existe une solution très élégante déjà opérationnelle pour certains traitements, et qui avance dans les centres de recherche pour prendre en compte tous les traitements possibles, c’est le chiffrement homomorphe.

 

Avec ce type de chiffrement, le Cloud n’est plus seulement un espace de stockage sécurisé mais devient également un espace de calcul et de consultation sécurisé. Il va vraiment servir, non seulement à héberger l’information sensible, mais aussi à l’utiliser … sans la sortir du Cloud. Seuls les résultats après traitements seront sortis pour être déchiffrés et exploités.

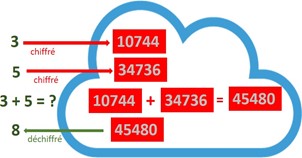
Dans le schéma ci-dessus, on veut obtenir le résultat de l’addition de deux nombres confiés chiffrés au Cloud, « 3 » et « 5 ». Mettons que le résultat homomorphe chiffré de 3 est « 10744 » et que le résultat homomorphe chiffré de 5 est « 34736 ».

Dans le Cloud s’opère l’addition homomorphe 10744 + 34736, qui donne 45480. Le déchiffrement homomorphe de 45480 donne … « 8 », ce qui est le résultat attendu.

C’est du moins ce qu’on souhaiterait en attendre, mais aujourd’hui le chiffrement homomorphe ne fonctionne que pour certaines opérations. Il ne permet pas, par exemple, de consulter une base

de données chiffrée pour obtenir le résultat souhaité en clair. Si un chiffrement dit « pleinement homomorphe » existait dès aujourd’hui, si tout traitement pouvait être réalisé sur les données chiffrées confiées dans un Cloud public, leur confidentialité et de leur intégrité seraient garanties. Mais on en est pas encore là, et les opérations qui peuvent déjà fonctionner posent quelques problèmes de performance, mais les recherches vont bon train pour offrir cette faculté inestimable.

Remarquons, sans verser trop dans la technique, et en simplifiant, que l’algorithme de chiffrement utilisé par le RSA, qui est à la base du chiffrement à clé publique, est, par nature, homomorphe pour la multiplication. En effet, le produit de deux nombres chiffrés est égal au chiffré du produit des deux nombres. Ce résultat, une fois déchiffré, est le même que si on fait la multiplication des deux nombres en clair. Un chiffrement homomorphe qui fonctionnerait pour l’addition ET pour la multiplication est appelé « chiffrement doublement homomorphe ». On s’en approche aujourd’hui, mais avec des problèmes de largeur des éléments chiffrés et de bruits numériques engendrés par les traitements. La difficulté du chiffrement homomorphe est de maintenir le « bruit numérique », que les opérations engendrent, au-dessous d’un seuil raisonnable sinon les algorithmes divergent et tout devient indéchiffrable. Nous n’étudierons pas ces problèmes complexes ici, mais nous pouvons espérer que les mathématiciens trouveront une solution élégante aux problèmes posés par le chiffrement doublement homomorphe.

Le chiffrement homomorphe ne doit pas être confondu avec le chiffrement cherchable qui permet de spécifier une procédure de déchiffrement à un résultat de calcul dans le domaine chiffré. Ce dernier type de chiffrement offre une solution pour consulter une base de données chiffrée, obtenir un résultat qui, déchiffré, donne le résultat attendu.

Comme application pratique, voyons comment le chiffrement homomorphe fournit une solution au vote par Internet. Nous ne parlons pas ici des machines de vote électronique, mais de l’électeur qui vote à partir de son navigateur.

Avec l’utilisation des algorithmes de El Gamal, le produit homomorphe des bulletins de votes chiffrés est égal à la somme homomorphe chiffrée des bulletins de votes. Les choix des votants ne sont jamais déchiffrés. A la clôture du scrutin, on effectue une multiplication homomorphique de tous les bulletins de votes. On obtient la somme chiffrée et on la déchiffre. Cette somme est donc le résultat des votes qui est obtenu immédiatement. Oui, le chiffrement homomorphe de El Gamal (entre autres cryptologues qui ont fait avancer cette technologie) permet cela.

Les bulletins sont chiffrés par la clé publique de l’urne, le déchiffrement de la somme des bulletins se fait par la clé privée de l’urne. Cette clé privée peut être répartie en plusieurs morceaux détenus par le président du bureau de vote et ses assesseurs. A l’ouverture du scrutin, le président et ses assesseurs reconstituent la clé de déchiffrement et obtiennent quasi immédiatement le résultat attendu.

Que le produit homomorphe des bulletins de votes chiffrés soit égal à la somme homomorphe chiffrée des bulletins de votes est une belle application de ce type de chiffrement.

Pour ceux qui aiment les formules mathématiques, si Ek(mn) est le bulletin de vote mn chiffré avec la clé publique k de l’urne :

Ek(m1) x Ek(m2) x … x Ek(mn) = Ek(m1 + m2 + … + mn)

Cette méthode est élégante dans sa simplicité d’utilisation. Les bulletins dans l’urne ne sont jamais déchiffrés pourtant on connaît le résultat de la somme des votes qui est d’ailleurs le seul renseignement qui est intéressant et non confidentiel après la fermeture du scrutin.

Cette méthode a déjà été utilisée pour les élections des représentants des Français résidant à l’étranger. Elle peut être utilisée aussi pour les élections des représentants du personnel ou dans les conseils d’administration des entreprises. Mais pour les élections présidentielles, sénatoriales ou législative, elle n’est pas autorisée en France. Nous ne parlons ici que du fondement cryptologique d’une application pratique d’un chiffrement homomorphe qui fonctionne. Le vote par Internet qui ne donne pas l’obligation de passer par un isoloir, et qui ne nécessite pas la cérémonie républicaine du dépouillement des votes, est-il à recommander ? C’est un débat intéressant, mais dans lequel nous ne prendrons pas parti ici.